HashMap qanday ishlaydi?

Ushbu maqolada HashMap tuzilmasini qanday ishlashi, uning ortidagi nazariya va zamonaviy dasturlash tillaridagi implementatsiyalarini batafsil tahlil qilamiz.

Muammo

Tasavvur qiling oddiy DNS server qurmoqchisiz. DNS serverning asosiy vazifasi berilgan domen nomi uchun, unga mos keladigan ip addressni topib berishdir. Masalan, foydalanuvchi 'google.com' uchun so'rov jo'natsa, unga mos ip address '8.8.8.8'ni qaytarish lozim.

Formalroq aytganda, quyidagi ikkita amalni bajaradigan struktura tuzishimiz kerak:

• insert(domen, ip) - berilgan domen uchun ip adresni ip etib belgilaydi.

• find(domen) - berilgan domen uchun mos ip adressni topib beradi.

Bunday strukturani qanday tuzish o'zimizga bog'liq, bunda asosiy e'tibor find va insert amallari tezligiga qaratiladi.

HashMapdagi "map"

Umuman shu kabi strukturalar, key-value map deb ataladi. Ya'ni, strukturada ma'lum kalitga(key) mos keluvchi bitta yoki bir nechta qiymatlar(value) saqlanadi:

domen (key)	ip (value)
google.com	8.8.8.8
cloudflare.com	1.1.1.1
example.com	1.2.3.4

Key-value map strukturasi kalitlarni qiymatlarga "bog'lam"ini saqlaydi. Bu bog'lam fanda mapping deb ataladi. Bizning misolimizda, DNS key-value strukturasi domen nomlarini ip addresslarga mappingini saqlaydi deyish mumkin.

HashMapdagi "map" so'zi ham aynan shuni bildiradi. HashMapni map qismini tushunib oldik, ana endi, asosiysi "hash" qismini tushunish. Bundan oldin, yuqoridagi muammo uchun bir nechta sodda va intuitiv bo'lgan yechimlarni ko'rib chiqamiz.

Sodda (Iterativ) yechim

Eng sodda yechimda, har bir (kalit, qiymat) juftligini oddiy listda saqlaymiz:

DNS_list = [
    ('google.com', '8.8.8.8'), 
    ('cloudflare.com', '1.1.1.1'), 
    ('example.com', '1.2.3.4')
]

Bu yechimda masalan, find('example.com') so'roviga javob topish uchun, 'example.com' kalitli list elementini topishimiz va undagi qiymatni(ip addressni) qaytarishimiz kerak. Listdan 'example.com'ni topish eng yomon holatda \(O(n)\) vaqt talab qiladi, chunki uni topish uchun butun listni ko'rib chiqishimizga to'g'ri keladi.

insert amali ham xuddi shu kabi \(O(n)\) vaqt oladi, sababi dastlab berilgan kalit listda allaqachon borligini tekshirishimiz lozim.

DNS serverimiz sekundiga minglab find so'rovlariga javob berishi kerak bo'lgani uchun, bu yechim samarali emas.

Balanced Binary Search Tree

BBST, ya'ni Balanced Binary Search Tree yuqoridagi insert va find amallarini \(O(log n)\) vaqtda amalga oshiradi. C++dagi map, Javadagi TreeMaplar aynan shu ma'lumotlar tuzilmasi orqali tuzilgan.

BBSTni qolgan yechimlardan ustun tarafi, unda elementlar kalit bo'yicha saralangan bo'ladi. Shuning uchun ham, ayrim qo'shimcha amallarni qo'llash mumkin. Masalan, agar qidirilayotgan kalitli element bo'lmasa, shu kalitga eng yaqin kalitni qiymatini \(O(log n)\) vaqtda topish mumkin.

Shuningdek, BBST quyida ko'radigan yechimlarimizdan farqli ravishda deterministik ishlash vaqtiga ega. Ya'ni amallarning ishlash vaqti kutilmaganda oshib ketmaydi va eng yomon holatda ham \(O(log n)\)ligicha qoladi.

Umuman olganda, bu yechimni jiddiy salbiy tomoni yo'q, tezlik jihatdan ham "yetarlicha" samarali. Masalan, to'plamda \(10^9\) ta element bo'lganda, Find amali javobni topish uchun \(~30\) ta operatsiya ishlatadi. Ammo, katta tizimlarda bu \(30\) ta amal ham ko'plik qiladi va bundanda tezroq yechimlardan foydalanishga undaydi.

Katta massiv usuli

Aynan shu yechim uchun tasavvur qiling, berilgan kalitlarni qiymati \([0..U]\) oralig'idagi butun son bo'lsin. Aytaylik, 'google.com' o'rniga \(1\) sonini, 'cloudflare.com' o'rniga \(0\) sonini va 'example.com' o'rniga \(2\) sonini ishlataylik.

Bunday imkoniyat bilan, yaxshiroq yechim topishimiz mumkin.

Dastlab, uzunligi \(U\) bo'lgan T[U] massiv yaratamiz. Massivning T[i] elementida \(i\) kalitga tegishli bo'lgan qiymatni saqlaymiz:

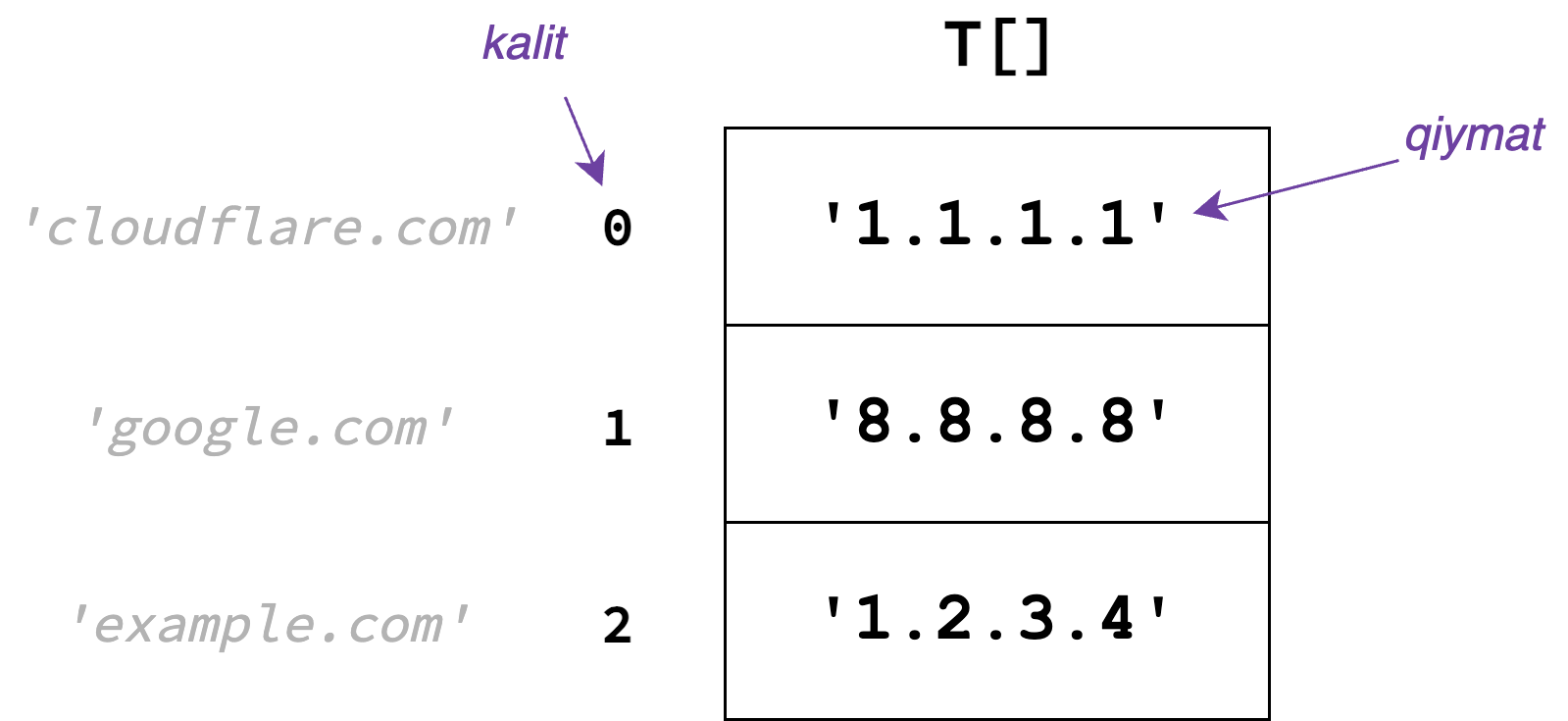
Ko'rib turganingizdek massiv indekslarini kalit sifatida, massiv elementlarini esa qiymat sifatida ishlatyapmiz. Bu esa bizga insert va find amallarini \(O(1)\) vaqtda amalga oshirish imkonini beradi. Sababi massiv elementlariga Random Access imkoni bor.

Hammasi zo'r!

Amalda esa kalitlar bunday zich holda, nomanfiy butun son ko'rinishida kelmaydi.

Hash Funksiya

Yuqoridagi muammoni hal qilish uchun 'google.com', 'example.com'larni yoki umuman ixtiyoriy ko'rinishdagi kalitlarni butun sonlarga o'tkazish yo'lini topsak kifoya.

Bu o'tkazishni amalga oshirish uchun esa Hash Funksiyadan foydalanamiz.

h(key) hash funksiyasi berilgan bo'lsa, u ideal holatda quyidagi shartlarni qanoatlantirishi lozim:

• h(key) funksiya, berilgan kalit key uchun, uning tipi va qiymatidan qat'iy nazar, shu keyga bog'liq \([0..B]\) oralig'idagi son qaytarsin.
• Berilgan key1 va key2 kalitlar uchun, agar key1 = key2 bo'lsa, h(key1) = h(key2) ham qanoatlantirilishi kerak. Ya'ni, google.com uchun, h('google.com') doim bir xil qiymat qaytarishi, izchil(consistent) bo'lishi lozim.
• Berilgan key1 va key2 qiymatlar uchun, agar key1 != key2 bo'lsa, h(key1) != h(key2) ham qanoatlantirilishi kerak. Ya'ni google.com va example.com uchun h() funksiya qaytargan qiymat bir xil bo'lib qolmasligi kerak. Boshqacha qilib aytganda, collisionlar bo'lmasligi lozim.
• h() funksiyani ishlash vaqti yetarlicha tez bo'lishi, to'g'rirog'i \(O(1)\) vaqtda ishlashi lozim.

Faqatgina shu shartlarni bajaradigan h() hash funksiya topganimizdan keyingina, amalda Katta Massiv usulidan foydalanishimiz va insert, find so'rovlariga \(O(1)\) vaqtda javob berishimiz mumkin.

Kutganingizdek, bunday ideal hash funksiya tuzishni imkoniy yo'q! Birinchi uchta shartni qanoatlantiradigan funksiya tuzgan taqdirda, 4-shartni qanoatlantirish imkonsiz.

4-shartni qanoatlantirish uchun esa bizga Randomness kerak!

Random Hash Funksiya

Random hash funksiya h(key), berilgan key uchun \([0..B]\) oralig'idagi tasodifiy sonni qaytaradi. Bunda hash funksiya, izchillikni saqlab qoladi, ya'ni h('google.com') doim tasodifiy lekin bir xil qiymat qaytaradi.

Random hash funksiyaga oddiy misol sifatida Polynomial Rolling Hashni keltirish mumkin. Berilgan s string uchun, h(s) ni qiymati quyidagicha bo'ladi:

\[ h(s) = s[0] + s[1] \cdot p + s[2] \cdot p^2 + ... + s[n - 1] \cdot p^{n-1} \mod B \]

Bu yerda \(p\) taxminan berilgan string alifbosi uzunligiga yaqin son bo'lishi kerak. Masalan, s satr faqat kichik lotin xarflaridan iborat bo'lsa, \(p\) ni qiymatini \(31\) qilib tanlash kifoya.

\(\mod B\) esa berilgan ifodani \(B\) ga bo'lgandagi qoldig'ini hisoblaydi. Bu esa funksiya \([0..B]\) oralig'idagi butun son qaytarishini kafolatlaydi.

E'tibor bergan bo'lsangiz, bu funksiya aslida random emas, balki deterministik holda ishlayapti. Amalda to'liq random hash funksiya tuzishni imkoni yo'q. Shuning uchun, yuqoridagi kabi random hash funksiyaga o'xshab ishlaydigan pseudorandom hash funksiyalar mavjud.

Collisionlar

Yuqoridagi random hash funksiya \(O(1)\) vaqtda ishlaydi(agar s ni uzunligi konstanta bo'lsa). Ammo, bunda collisionlar bo'lishi mumkin, ya'ni ikkita turli kalit uchun hash funksiya bir xil qiymat qaytarishi mumkin. Bu esa HashMap to'g'ri ishlashiga to'sqinlik qiladi.

Bu muammoni quyidagi Hash Table strukturasi orqali hal qilamiz.

Birthday Paradox

Xonada \(n\) ta odam bor, ular ichida ixtiyoriy ikkitasini tug'ilgan kuni bir xil bo'lishini ehtimolligi \(50\%\) dan oshishi uchun, \(n\) ni qiymati qanday bo'lishi kerak?

Bu masalaning javobi, shunchalik mantiqqa zid bo'lganidan, uni Birthday Paradox deb aytishadi. Sababi, xonada \(23\) ta odam bo'lganda, ixtiyoriy ikki odamni tug'ilgan kuni bir kunda bo'lib qolishi ehtimolligi 50% dan oshadi. Bir yilda \(365\) kun bo'lsada, bor yo'g'i \(23\) ta odam bilan kunlar to'qnashishi ehtimoli \(50\%\) dan oshadi.

Bu masala bizga collisionlarni tushunishda yordam beradi. Ya'ni, \(B\) ni qiymatini \(365\) etib belgilab, \(23\) ta satrni hash qiymatini to'liq random hash funksiya orqali olsak, ikkita satrni hash qiymati bir xil bo'lish ehtimoli \(50\%\) dan ortiq bo'ladi. Tushunish uchun, agar \(B\) ni qiymatini \(10^9\) qilib olganimizda ham, bor yo'g'i \(40 000\) ta satr bilan, \(50\%\) collision ko'rsatkichiga ega bo'lardik.

Bu degani hash funksiya qiymatlar sohasi \(B\) ni kattalashtirish foyda bermaydi.

Collisionlardan qochish emas, ularni hal qilish lozim.

Hash Table

Katta Massiv usuli va random hash funksiyalarni bitta qilib, Hash Table strukturasini quramiz.

Hash Table \(0\) dan \(B\) gacha indekslangan \(T[]\) massivdan iborat. Berilgan kalit \(s\) uchun dastlab h(s) qiymatini topamiz va u qaytargan hash qiymatni indeks sifatida ishlatamiz:

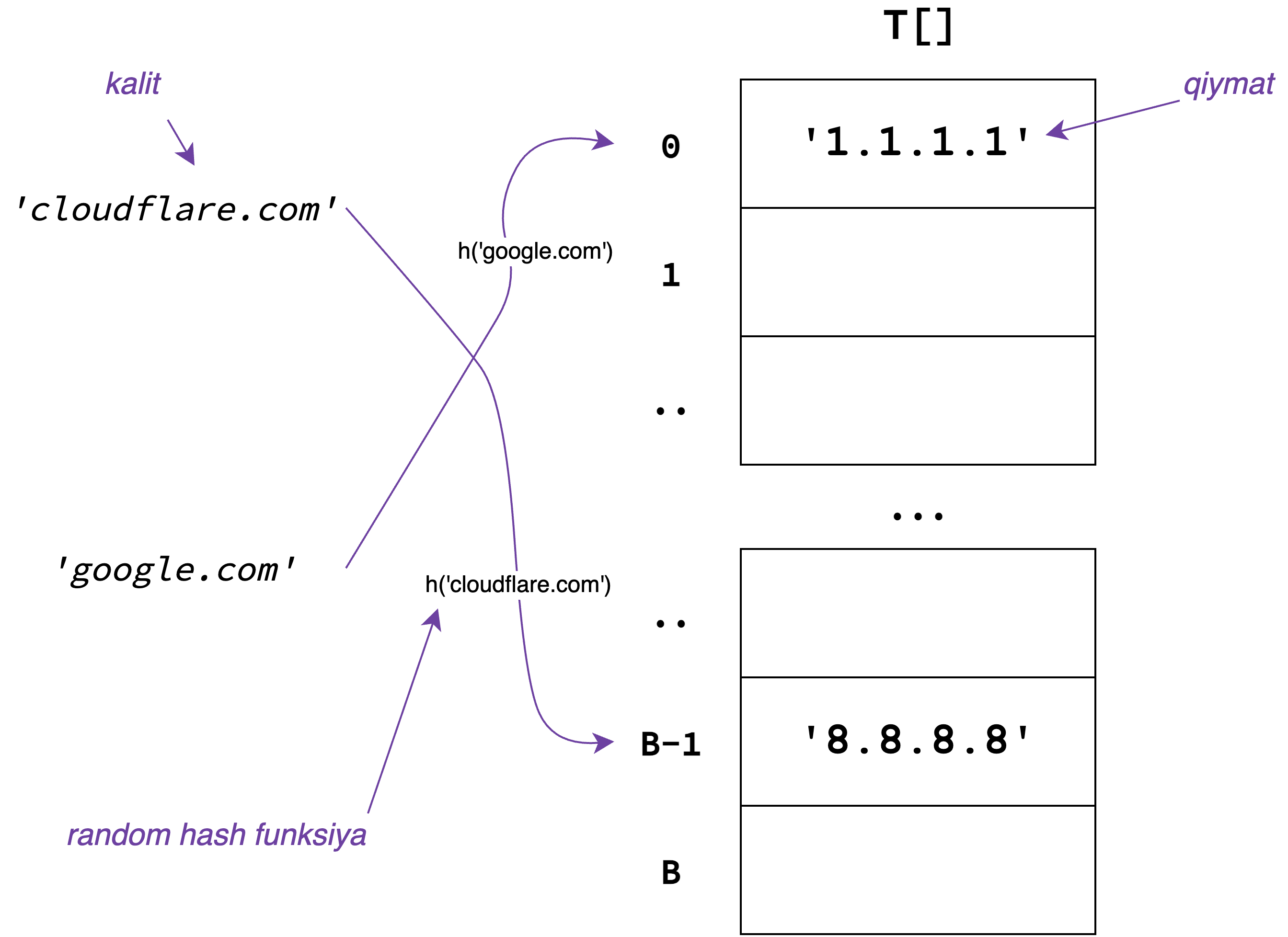
h(s) funksiya \(O(1)\) da ishlashini inobatga olsak, bu Hash Table strukturasi orqali find va insert amallarini ham \(O(1)\)da amalga oshirishimiz mumkin bo'ladi. Bunga albatta collisionlar to'sqinlik qiladi:

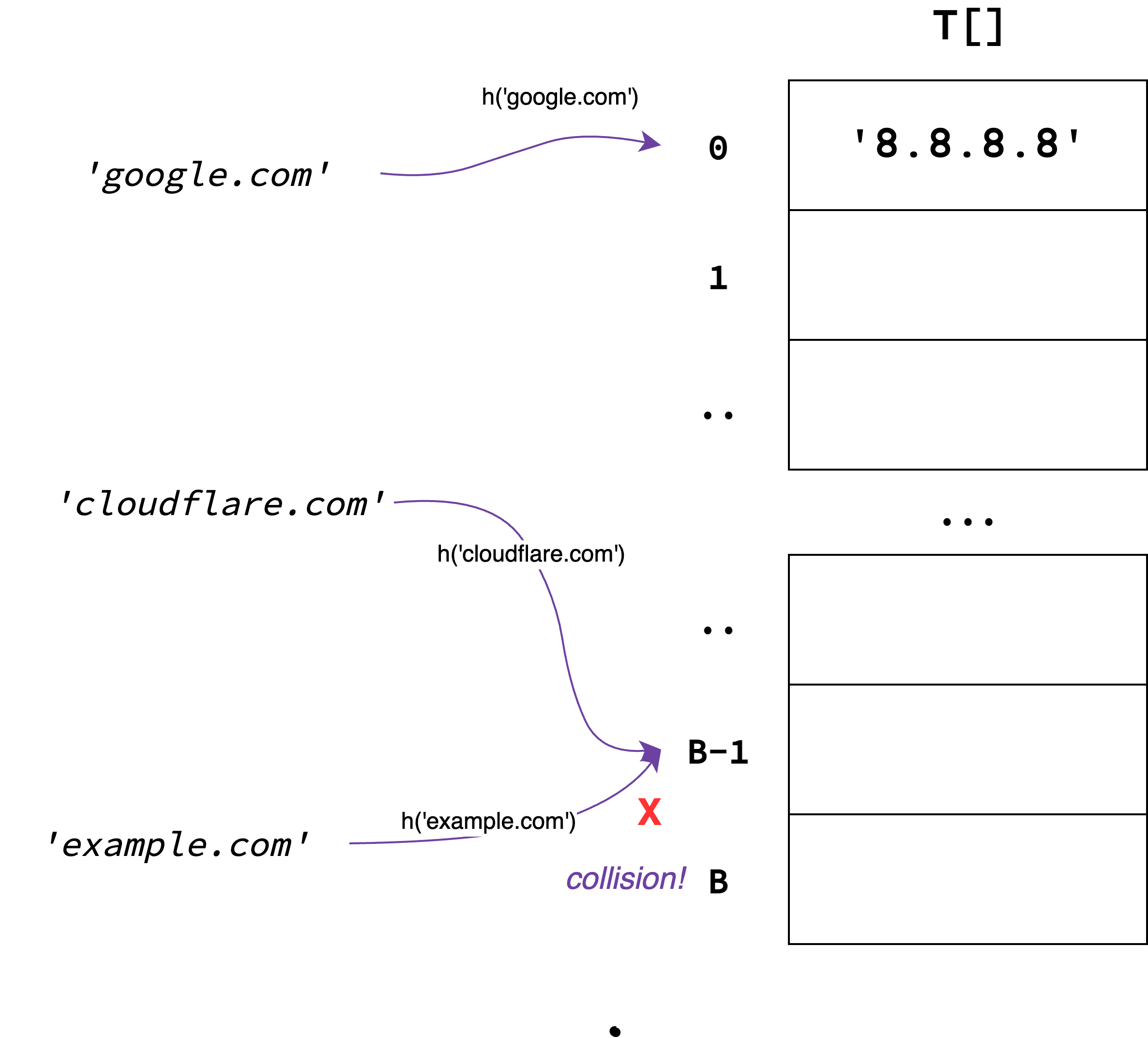
Yuqoridagi holatda 'cloudflare.com' bilan 'example.com' kalitlari o'z qiymatlarini bir xil indeksda saqlayapdi. Bu eas find va insert amallari to'g'ri ishlashiga to'sqinlik qiladi.

Quyida collisionlarni qanday hal qilish mumkinligini ko'rib chiqamiz.

Chaining

Collisionlarni boshqarishni eng mashhur usullaridan biri bu Chaining. Uning g'oyasi juda ham oddiy. Hash Tableni har bir indeksida to'g'ridan to'gri qiymatni emas, bir nechta qiymatlarni o'z ichiga olgan linked-listni saqlaymiz:

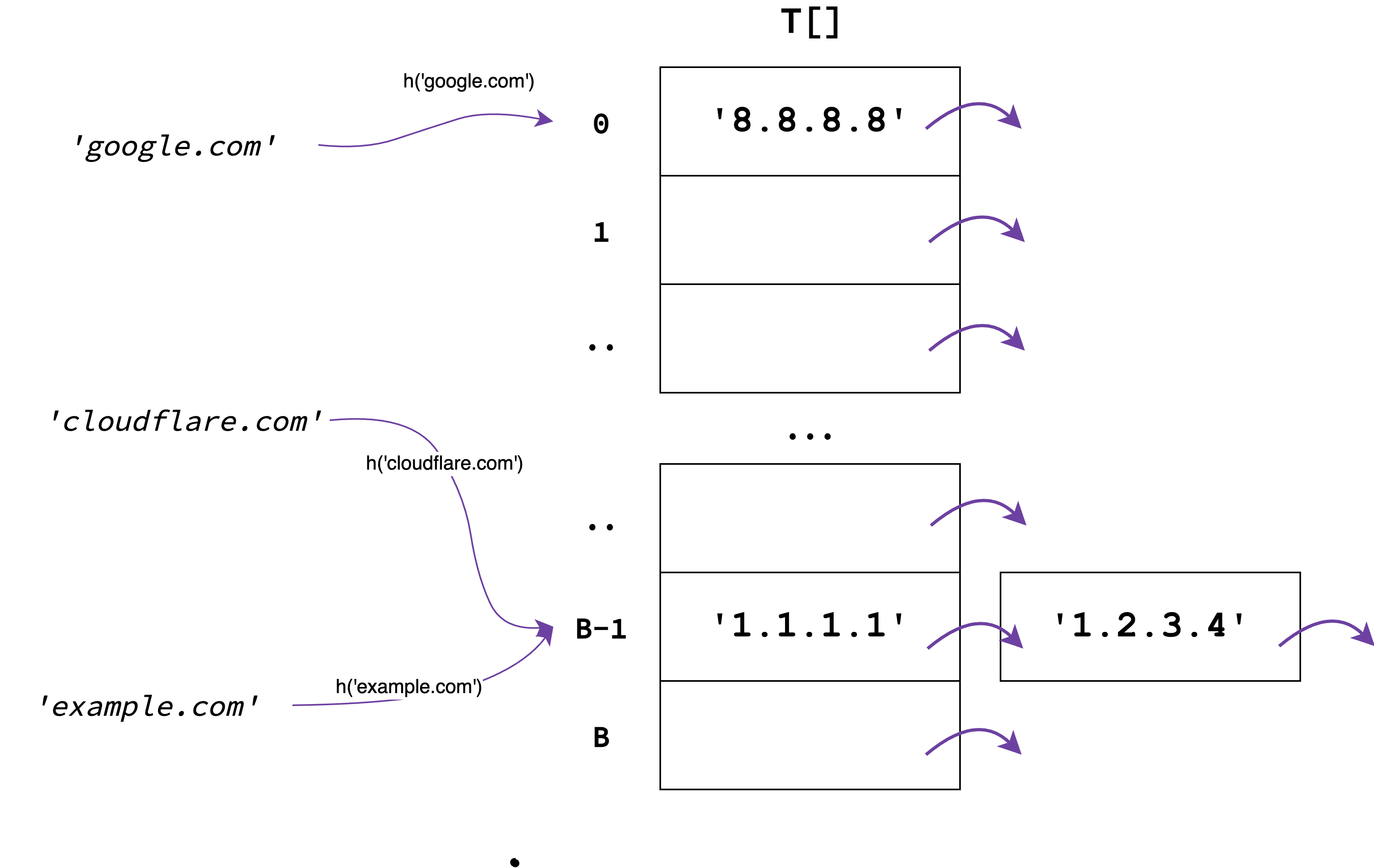
Ana endi, 'cloudlfare.com' va 'example.com' kalitlari uchun collision bo'lsada, ularning qiymatlarini alohida linked-list elementi sifatida saqlaganimiz uchun bu kalitlarni va ularni qiymatlarini to'g'ri ishlatishimiz mumkin.

insert va find funksiyalarini esa quyidagicha amalga oshiramiz:

• insert(key, value) chaqirilganda, T[h(key)] katakdagi linked-listni oxiriga valueni qo'shib qo'yamiz.

• find(key) uchun esa, T[h(key)] katakdagi linked-list elementlarini iterativ tarzda ko'rib chiqib, o'zimizga kerakli qiymatni qaytaramiz.

Ana bo'lmasa, \(O(1)\) lik yechim qidira turib, iterativ ishlaydigan algoritmni ko'ryapmiz. Hamma kalitlar tengdaniga collision bo'lib, qaysidir katakdagi linked-list juda ham uzun bo'lib ketsachi? Haqiqatdan ham bu holda Hash Table \(O(n)\) vaqtda ishlaydimi?

Bu savollarga javob berish uchun matematikani chaqiramiz!

Ishlash vaqti analizi

Dastlab, analiz uchun quyidagi o'zgaruvchilarni takrorlab o'taman:

• \(S\) - HashMapda hozirda turgan kalitlar to'plami

• \(n\) - \(S\) ning uzunligi, ya'ni HashMapdagi elementlar soni

• \(B\) - Bucket size, ya'ni Hash Tableni uzunligi yoki linked-listlar soni

• \(h(key)\) - \(key\) kalit uchun [\(1\)..\(B\)] oralig'idagi Hash Qiymatni qaytaruvchi random hash funksiya

• \(T\) - Hash Table strukturasi, \(T[i]\) element Hash Qiymati \(i\) bo'lgan elementlarni saqlovchi linked-listdan tashkil topgan.

Agar collisionlar bo'lmaganida find amali \(O(1)\) vaqtda ishlar edi. Ammo, collisionlarni hisobga oladigan bo'lsak, ishlash vaqti bo'yicha endi bu kafolatni bera olmaymiz. Yangi yechimda, find(key) quyidagi asimptotikaga ega bo'ladi:

\[ O(1 + size(T[h(key)])) \]

Ya'ni berilgan kalit uchun hash qiymat h(key)ni topamiz, find amali shu indeksdagi linked-list ustida iteratsiya qilgani uchun, umumiy amallar soni linked-list uzunligiga teng bo'ladi.

("1 + " yozilishini sababi, linked-list uzunligi 0 bo'lganda, asimptotika \(O(0)\) bo'lib qoladi va bunday bo'lishi mumkin emas).

Matematik kutilma

Bu formula ma'noga ega bo'lishi uchun linked-list uzunligi qanday bo'lishini bilishimiz kerak. Avvalroq aytilganidek, algoritm deterministik bo'lmagani uchun, bu qiymatni aniq aytib yoki formulaga solib bo'lmaydi. Shu bois, findni ishlash vaqtini emas, uning ishlash vaqtini matematik kutilmasini topamiz.

Buning uchun dastlab quyidagi indicator random variableni belgilaymiz:

\[ \begin{equation} \phi_x= \begin{cases} 1, & h(x) = h(key) \text{ bo'lsa,}\ \\ 0, & \text{aks holda} \end{cases} \end{equation} \]

Ya'ni, qandaydir \(x\) kalitni hash qiymati berilgan kalit \(key\) bilan mos kelib qolsa, \(\phi_x\) ni qiymati \(1\), aks holda \(0\) bo'ladi.

Dastlab ishlash vaqtini shu qiymat orqali yozamiz:

\[ O(1 + \displaystyle\sum_{x \in S} {\phi_x}) \]

Bu formulada, linked-list uzunligini berilgan hash qiymatga mos keladigan kalitlar soni orqali ifodalayapmiz xolos.

Aniq ishlash vaqtini topishni iloji bo'lmagani uchun, yuqoridagi formulani matematik kutilmasini topamiz:

\[ \mathbb{E}[1 + \displaystyle\sum_{x \in S} {\phi_x}] \]

Matematik kutilmaning chiziqlilik hossasiga ko'ra, yuqoridagi formulani quyidagicha yozish mumkin:

\[ 1 + \displaystyle\sum_{x \in S} {\mathbb{E}[\phi_x]} \]

"Indicator random variable"ni matematik kutilmasi, uning qiymati \(1\) bo'lishi ehtimolligiga teng, ya'ni:

\[ \mathbb{E}[\phi_x] = \mathbb{P}[\phi_x = 1] \]

Bu ehtimollik, qandaydir x kalit, berilgan \(key\) kalit bilan bitta hash qiymatga tushib qolish ehtimolligini bildiradi. Uni qiymatini esa quyidagicha topamiz:

\[ \begin{equation} \mathbb{P}[\phi_x = 1] = \begin{cases} 1, & x = key \text{ bo'lsa,}\ \\ 1/B, & \text{aks holda} \end{cases} \end{equation} \]

Agar kalitlar bir xil bo'lsa, ehtimollik \(1\) bo'ladi, aks holda, \(x\) kalitni hash qiymati aynan \(key\) kalit hash qiymatiga to'g'ri kelishi ehtimoli \(1/B\), chunki \(B\) ta tanlovdan aynan bittasi mos kelishi kerak.

Bu ehtimollikni formulaga yozsak, quyidagi natijaga yetib kelamiz:

\[ 1+\displaystyle\sum_{x \in S}{\mathbb{P}[\phi_x = 1]} = 1 + 1 + (n-1)/B = 2 + (n-1)/B \]

Big O notationni qaytarsak, umumiy ishlash vaqtini:

\[ O(1 + n / B) \]

kabi yozish mumkin.

Xulosa qilib aytganda, Hash Tabledagi Bucket Size \(B\) ni \(n\) dan kattaroq qilib tanlasak, ishlash vaqtini matematik kutilmasi (yoki expected running time) \(O(1)\) bo'ladi!

Amortizatsiya

Afsuski, \(n\) ni qiymatini oldindan bilmaymiz. HashMapga ko'proq element qo'shilgani sari, uning qiymati o'zgarib turadi. \(n\) ni qiymati qanday bo'lishidan qat'iy nazar juda katta \(B\) qiymat tanlab qo'yish ham yaramaydi, xotiradan ortiqcha ko'p joy egallab qo'yamiz. Doimgidek, eng oddiy yechimni o'ylaymiz!

Dastlab, \(B\) ni qiymati uchun kichikroq biror bir sonni tanlaymiz, aytaylik 100. Endi tasavvur qiling, HashMapga elementlar qo'shilib, uning hajmi 100 ga yaqinlashib qoldi. Bu yaxshi emas, \(n\) ni qiymati \(B\) dan oshib ketmasligi kerak, aks holda \(O(1)\) vaqtni kafolat qila olmaymiz. Shuning uchun, \(n\) ni qiymati \(B\) ga yaqinlashganda, \(B\) ni uzunligini ikki barobar oshiramiz.

Bu oson ish emas, \(B\) ni qiymati o'zgarganda eski hash qiymatlar ma'noga ega bo'lmay qoladi, shuning uchun butun boshli Hash Tableni \(B\) ni yangi qiymati bilan qaytadan quramiz. Ha, Hash Table qancha katta bo'lmasin, bu ishni qilishga majburmiz.

\(B\)ni qiymatini oshirish ortiqcha ishlarni ko'paytirib tashladi. Aslida esa ishlash vaqti baribir \(O(1)\)! Alohida bir so'rovni olib qaraganda, ishlash vaqti \(O(n)\) bo'lib ketishi mumkin, lekin Amortized analysis qiladigan bo'lsak, ya'ni bir nechta so'rovlarni umumiy olib qaraydigan bo'lsak, har bir so'rov uchun bajariladigan amallar \(O(1)\) ligini isbotlash mumkin. Buni qisqacha intuitiv sababi, \(B\)ni uzunligini ikki barobar kattalashtirish amali aslida juda kam miqdorda amalga oshadi va shuning hisobiga Hash Tableni har safar yangidan qurish ishlash vaqtiga ta'sir qilmaydi.

Xulosa

Demak, find(key) amalini ishlash vaqti:

\[ O(1) \]

Lekin bu vaqt, oddiy "running time" emas, amortized expected running time. Tarjima qilmay qo'yaverdim, muhimi \(O(1)\)ni \(O(1)\)dan farqi bor.

Amaldagi ishlash vaqti

Yuqoridagi analizda biz faqat nazariy jihatdan ishlash vaqtini ko'rdik. Aslida xatto "Big O notation"dagi asimptotika ham amaldagi ishlash vaqtini to'laligicha aniq ko'rsatib bera olmaydi. Analizlarning barchasi approksimatsiyaga asoslangan.

Bizdagi approksimatsiya esa oddiy Big O emas, matematik kutilmadagi va amortizatsiyadagi Big O. Matematik kutilma, o'rtacha holatdagi ishlash vaqtini ko'rsatib beradi xolos. Bu esa amalda unchalik ham foydali emas, ko'plab so'rovlar bu o'rtacha qiymatdan ancha ko'proq vaqt olishi mumkin.

Amortizatsiyada ham shunaqa, nazariy jihatdan ishlash tezligi o'zgarmasada, amalda amortizatsiya yaxshi ishlashi uchun yetarlicha ko'p so'rovlar ishlatilishi lozim.

Amalda, bundan tashqari yana ko'plab faktorlarni inobatga olish lozim. Ularni yaxshiroq tushunish uchun, HashMapni zamonaviy dasturlash tillaridagi implementatsiyalarini ko'rib chiqamiz.

Java HashMap implementatsiyasi

Java HashMap uchun yuqorida biz ko'rgan usuldan foydalanadi. Hash Funksiya o'rnida obyektning hashcode() qiymatini ishlatadi. Collision uchun esa yuqorida ko'rsatilgan "Chaining" usulidan foydalanadi.

Rehashing

Amortizatsiya bo'limida aytib o'tilganidek, Bucket o'lchami HashMap o'lchamidan iloji boricha kattaroq bo'lishi lozim. Buni ta'minlash uchun, HashMap kattalashgani sari Bucket o'lchamini ikki barobar oshirish usulini ko'rib chiqqan edik, bu usul Javada Rehashing deb nomlangan.

Rehashing asosan ikkita parameterga bog'liq.

• initial capacity - Bucket o'lchami \(B\) ni dastlabki qiymati.

• load factor - Hash Table qay darajada to'lganda Rehashingni amalga oshirish kerakligini bildiruvchi qiymat. Birlamchi qiymati 0.75 va ko'p hollarda vaqt va xotira sarfini muvozanatda ushlab turadi.

Load factor kichikroq bo'lsa, Rehashing ko'proq bo'lib, so'rovlar uchun Bucket o'lchami kattaroq bo'ladi. Bu degani collision kamroq bo'lib, find funksiyasi tezroq ishlaydi. Yomon tomoni, Bucket o'lchami keragidan ortiq katta bo'lib, xotiradan keragidan ko'p joy talab qiladi. Shuningdek, Rehashinglar sonini ko'paytirish ham xavfli, aks holda asosiy vaqt findga emas Rehashingga ketib qoladi.

Load factor kattaroq bo'lganda esa, kamroq Rehashing sodir bo'ladi va Bucket o'lchami xotiradan ortiqcha ko'p joy egallamaydi. Ammo, collisionlar soni oshib, find funksiyasi sekinroq ishlashiga to'g'ri keladi.

Shuningdek, HashMap elementlarini iteratsiyasi uchun ketadigan vaqt HashMap sig'imiga proporsional. HashMap sig'imi Bucket o'lchami + HashMapdagi elementlar soniga teng. Shuning uchun, Bucket o'lchamini keragidan ortiq katta qilib yuborish iteratsiya tezligiga ham ta'sir o'tkazadi.

Treeify

Java 8 dan boshlab, HashMap implementatsiyasiga yana bir optimizatsiya qo'shilgan.

Bucketlarda endi faqat linked-listlar emas, BBST lar ham ishlatilishi mumkin.

Ya'ni, bucketdagi elementlar soni maxsus qiymat TREEIFY_THRESHOLDdan o'tib ketsa, ushbu bucketda linked-list o'rniga o'zini balanslovchi binar qidiruv daraxtlari(BBST) ishlatiladi. Linked-listda element qidirish \(O(n)\) vaqt talab qiladi, BBSTda esa \(O(log n)\).

TREEIFY_THRESHOLDning qiymati 8 ga teng deb belgilangan. Ya'ni, Bucketdagi linked-list uzunligi 8 dan oshib ketsa, linked-list o'rniga daraxt quriladi.

Bu qiymat, kichik bo'lsada, amalda linked-list uzunligi deyarli bu darajaga yetib bormaydi. Random hash funksiya ishlatilganda 8 ta qiymat bitta bucketga tushib qolish ehtimolligi juda ham kichik.

HashMapni implementatsiyasida bu haqida qiziq komment bor:

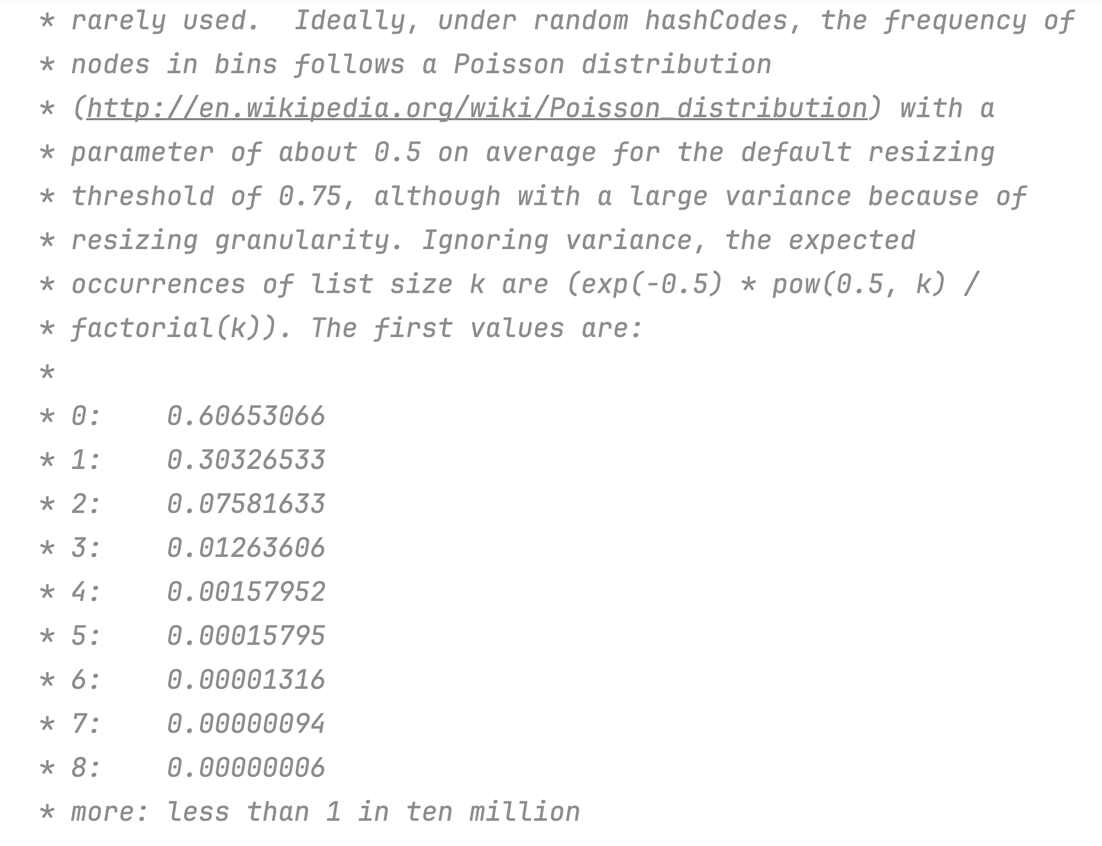
Xullas, 10 milliondan bitta holatda Treeify ishlashi mumkin.

Python Dictionary

Python ham Dictionary uchun Hash Funksyialardan foydalanadi. Ammo uning Hash Table strukturasi Javanikidan tubdan farq qiladi.

Open Addressing

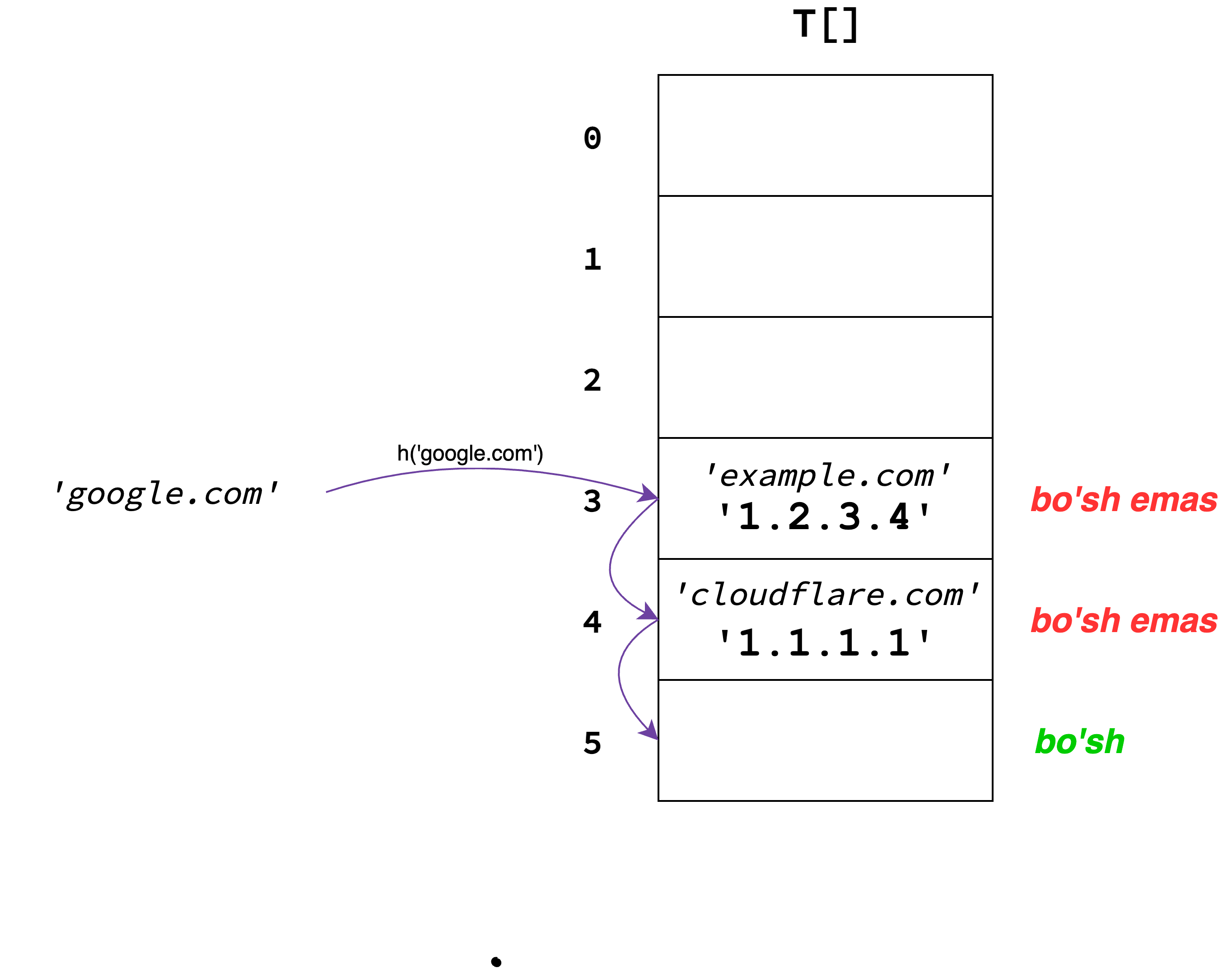
Chaining usulida collision bo'lishiga yo'l qo'yib berib, collision bo'lgan kalitlarni umumiy qilib hal qilgan edik. Collision bo'lishiga boshidanoq yo'l qo'ymasakchi?

Umuman collisionsiz ishlaydigan hash funksiyalar tuzish mumkin, lekin bu hash funksiyalar yetarlicha samarali emas, \(O(1)\) vaqtda ishlaydigan hash funksiyalarda esa doim collision bo'ladi. Gibridroq yechim o'ylab ko'rsakchi, hash qiymatlarni topish uchun hash funksiyalardan foydalanamiz, lekin collision bo'lgan payti, kalit uchun boshqa bo'sh bo'lgan bucketni topib beramiz. Bucketlar soni elementlar sonidan ko'p bo'lganda, bu algoritmda collision bo'lmaydi. Shu kabi ishlaydigan struktura Open Addressing deyiladi.

Open addressing Hash Table uchun oddiy T massiv ishlatadi, ya'ni T dagi har bir bucketda bitta element saqlanadi xolos.

Berilgan kalitga mos bucketni topish uchun, dastlab h(key) hash funksiya qiymati aniqlanadi va shu indeksdagi bucket tekshiriladi. Bucket bo'sh bo'lsa, berilgan kalit shu bucketga map qilinadi. Bucket bo'sh bo'lmasa, keyingi bucket tekshiriladi va hokazo:

insert(key)ni quyidagicha tariflash mumkin:

i = h(key)
while T[i] != null:
    i ++
T[i] = key

find(key) ham shunga o'xshash:

i = h(key)
while T[i] != null and T[i] != key
    i ++
return T[i]

E'tibor bering, bu yerda find uchun oddiygina qilib T[h(key)]ni qiymati qaytarilmayabdi. Sababi h(key) pozitsiyada hali ham collision bo'lishi mumkin. Hash Tableda collision yo'q degani, hash funksiyada collision yo'q degani emas. Shuning uchun, hash qiymatni olgandan keyin bizga kerakli kalitni topmaguncha keyingi bucketlarni tekshirib borishimizga to'g'ri keladi.

Shu kabi qadamma qadam tekshirish amalga oshirilgani tufayli, bu usul odatda probing deb ham ataladi.

Linear probing

Aynan yuqoridagi probing usuli linear probing deb ataladi. Ya'ni, hash qiymatni topgandan keyin, bo'sh bucket topilguncha chiziqli tarzda keyingi bucketlar tekshirib boriladi.

Nazariy jihatdan bu usul \(O(1)\) vaqtda ishlaydi, lekin ishlash vaqti hash funksiyaga juda ham bog'liq. Ishlatilgan hash funksiya yetarlicha random bo'lishi lozim. Hash funksiya yetarlicha random bo'lmasa, bu usul primary clustering deb nomlanuvchi muammodan aziyat chekadi. Ya'ni bir marta qaysidir bucketlar ketma-ketligi to'lib qoldimi, bu ketma-ketlik borgan sari yiriklashib boraveradi. Ketma-ket to'lib qolgan bucketlar to'plami qnacha o'sgani sari, yana o'sish ehtimoli oshib boraveradi. Shuning uchun, hash funksiya oz bo'lsa ham random bo'lmasa va ko'proq collisionlar bo'lishni boshlasa, clustering o'lchami birdaniga tez o'sib ketadi. Bu degani shu bilan birga ishlash vaqti ham birdaniga sekinlashadi.

Afsuski, amalda bu kabi to'liq random hash funksiya tuzishni imkoni yo'q.

Pseudorandom probing

Linear probingda hash funksiya yetarlicha random bo'lmagani uchun kalitlar to'planib "cluster"lar hosil qilayotgan edi. Bu muammoni yanada ko'proq randomness orqali hal qilamiz!

Pseudo-random probingni g'oyasi oddiy. Collision bo'lgan kalit uchun bucket qidiryotganda, bucketlarni birin-ketin emas, random tartibda tekshiramiz. Shunda yuqoridagi kabi primary clustering muammosi bo'lmaydi.

Buning uchun "probing sequence" deb ataluvchi ketma-ketlik tuzib olamiz. Bu ketma-ketlikni birinchi elementni hash(key) qiymatiga teng bo'ladi. Qolgan elementlari esa oldingi elementga asoslanib qandaydir boshqa random indeks bo'ladi. Shuningdek, bucketlar soni B bo'lsa, "probing sequence"da \([0..B-1]\) oralig'idagi sonlar aniq 1 martadan uchraydi, ya'ni bu ketma-ketlik elementlari takrorlanmaydi. Probing uchun bu muhim xossa hisoblanadi.

Misol sifatida quyidagi "probing sequence"ni ko'raylik:

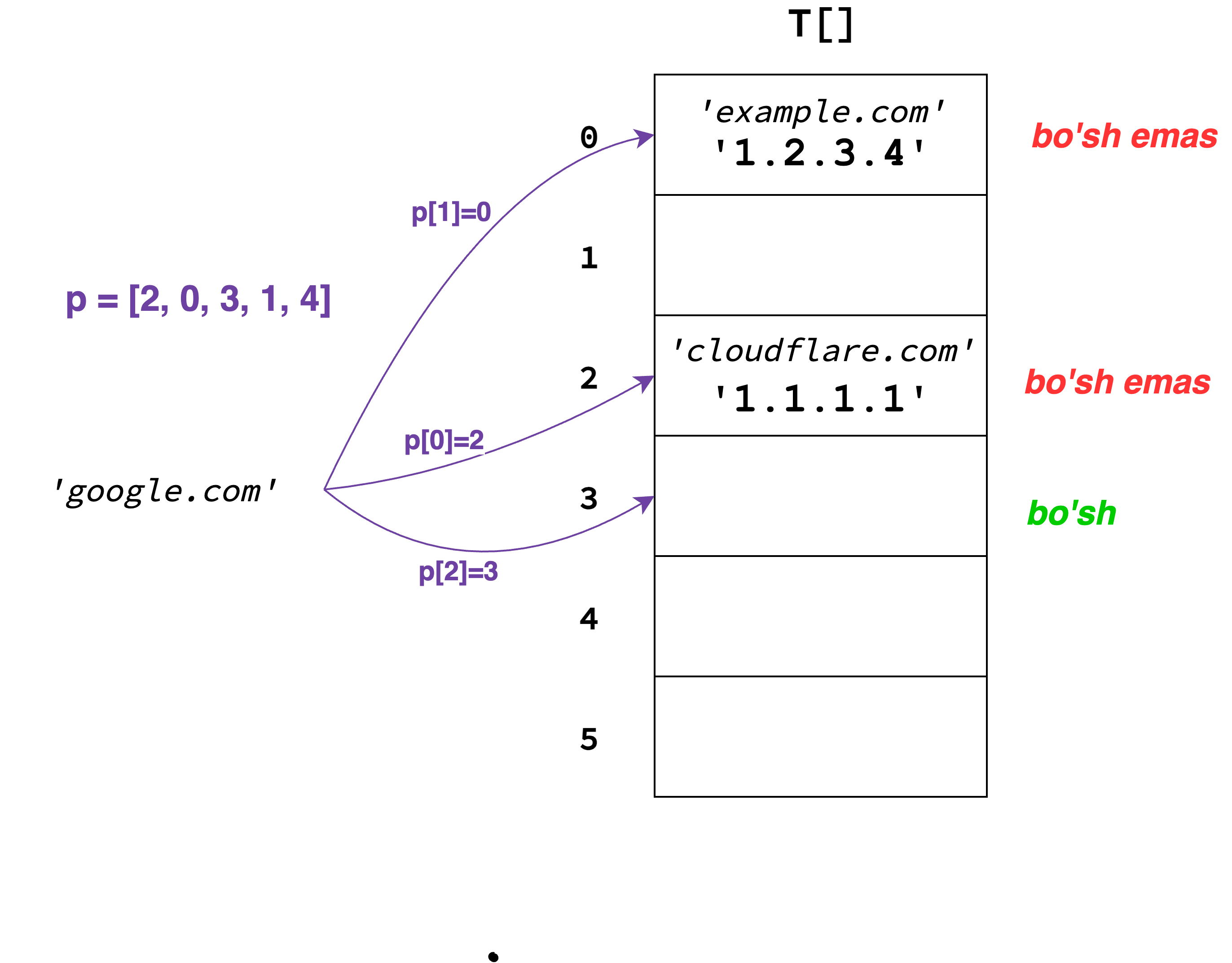
Bu yerda, h("google.com") ni qiymati \(3\) edi(o'z o'zidan \(p[0]\)ni qiymati ham). Bu orqali, probing sequence \(p = [2, 0, 3, 1, 4]\) tuzib olindi. Algoritm endi shu tartibda bo'sh bucketni qidiradi. Dastlab 2-bucketni tekshiradi, so'ng 0-, so'ng 3-bucketni va hokazo. Bo'sh bucket topilganidan so'ng, kalit o'sha bucketga qo'yiladi.

Probe sequenceni qurish uchun "Pseudorandom son generatori"dan foydalansak bo'ladi. Oddiyroq qilib aytganda probe ketma-ketlikni quyidagicha rekursiv formula orqali ifodalash mumkin:

\[ p[0] = h(key) \hspace{2.5cm} \]

\[ p[i] = (a * p[i - 1] + c) \% B, \hspace{1cm} i = 1..n - 1 \]

\(p\) ni elementlari takrorlanmasligini kafolatlovchi mos \(a\) va \(c\) qiymatlarni topish mumkin.

Afsuski, random probingni ham kichik bir kamchiligi bor. E'tibor bergan bo'lsangiz, probing ketma-ketlikni qiymatlari faqat \(p[0]\) ga bog'liq, ya'ni ikkita ketma-ketlikni \(p[0]\) qiymati bir xil bo'lsa, qolgan qiymatlari ham bir xil bo'ladi. Bu esa collision bo'ladigan kalitlarda linear probingdagi kabi muammoga sabab bo'ladi, bu muammo secondary clustering deb ataladi.

Amalda bu muammoni Double Hashing usuli orqali hal qilish mumkin. Ammo, quyida Pythonni qiziq yechimini ko'ramiz.

Pythondagi probing

Probing uchun hash funksiya qancha random bo'lsa shuncha yaxshi degan xulosaga keldik. Ajablanarli jihati, pythondagi hash(key) funksiya u qadar random emas. Masalan, butun sonlarni hash qiymati sonni o'ziga teng:

>>>[hash(i) for i in range(4)]
[0, 1, 2, 3]

Bu orqali bir nechta ketma-ket sonlarni hash qiymatlarini topish juda ham tez va collisionlarsiz amalga oshadi, randomlikdan esa asar ham yo'q! Amalda esa sonlar juda ham ko'p ishlatiladi va bu kabi yechim umumiy random yechimlardan ko'ra tezroq ishlaydi.

Ammo, hash() funksiyani random emasligi, turli zaifliklarga sabab bo'lishi mumkin. Masalan, collision bo'ladigan kalitlarni juda osonlik bilan generatsiya qilish mumkin.

>>> mod = 2**61-1 (Mersen tub soni)
>>> hash(mod)
0
>>> hash(mod**2)
0
>>> hash(mod**3)
0
>>> hash(mod**4)
0
>>> hash(mod**5)
0
>>> ...

Hash funksiya shu darajada zaif bo'lgani uchun, yaxshiroq probing mexanizmidan foydalanish talab etiladi. Shuning uchun Python pseudo-random probingni o'zgartirilgan versiyasini ishlatadi. Pythonda ishlatilgan probing sequence quyidagi rekursiv formuladan iborat:

\[ p[i] = (5 * p[i - 1] + perturb) \hspace{0.2cm} \% \hspace{0.2cm} B \]

Bu formulaning oddiy formuladan asosiy farqi perturb qiymatdadir. Perturbning qiymati odatda hash(key) ning oxirgi 5 ta bitini o'chirib tashlagandan keyingi songa teng bo'ladi. Ya'ni, pseudo-random son generatorida har doim konstant qiymat ishlatishni o'rniga, kalitni qiymatiga bog'liq bo'lgan qandaydir "noise" qiymat ishlatiladi. Bu secondary clustering muammosini hal qilishda yordam beradi.

Linear probing baribir yaxshiroqmi?

Real hayotda shuncha qilgan analiz va hisob kitoblarimiz ham to'liq hikoyani aytmaydi. Dasturimizda ishlatyotgan qiymatlarimizni hammasi ham to'g'ridan-to'g'ri asosiy xotira (RAM)dan olinmaydi. Odatda RAMdan oldin bir nechta "Cashe memory" ya'ni Kesh xotira ishlatiladi. RAMdan ma'lumot o'qish uchun 100 nanosekund vaqt ketsa, eng yaqin Keshdan ma'lumot o'qish 1 nanosekundni tashkil qiladi. Ma'lumotni qaysi xotiradan o'qiganimiz ishlash tezligida 100 martalik farqni yuzaga keltiryapti.

Kesh xotiradan ko'proq va unumliroq foydalanish uchun locality degan tushunchadan foydalanish lozim. Oddiy misol, berilgan massiv elementlarini birin-ketin iteratsiya qilib ishlatish, elementlarni tasodifiy tartibda ishlatishdan ko'ra ancha tezroq ishlaydi. Sababi, bitta massiv elementi ishlatilganda, protsessor nafaqat shu elementni, balki shu elementdan keyingi bir qancha baytlarni Kesh xotiraga ko'chiradi. Masalan 1-elementga murojaat qilinganidan so'ng, 2-, 3- va keyingi bir nechta elementlar allaqachon Keshda bo'ladi va ularga murojaat qilish ancha tez amalga oshadi.

Bu misol sizga allaqachon tanish tuyulgan bo'lsa kerak, linear probingda random probingga nisbatan locality yaxshiroq. Collisionlar ko'payib bir joyga to'planib qolgan taqdirda ham bucketlarga murojaat qilish juda ham tez amalga oshadi, chunki bucketlarni iteratsiya qilish jarayoni locality xususiyatiga ega. Random hashingda esa unday emas, bitta bucket ishlatilganidan so'ng, keyingi bucket Kesh xotirada bo'lishiga kafolat yo'q.

Shunday qilib, amalda linear probing boshqa probinglarga nisbatan ancha yaxshi ishlashi mumkin, lekin baribir ishlatilgan hash funksiya qancha random bo'lsa shuncha yaxshi. Pythonda esa hash funksiyalar qastdan yetarlicha random qilinmagan, shu sababli linear probingni ishlatishni imkoni yo'q.

Chaining yoki Open Addressing?

Ikkala usuldan yaxshirog'ini tanlash qiyin va ishlatilish sohasiga juda ham bog'liq.

Chainging linked-list ishlatgani uchun biroz xotiradan ko'p joy oladi va Kesh xotiradan unumli foydalanmaydi. Open Addressingda esa, ayniqsa linear probing ishlatilganda Kesh xotira juda ham samarali ishlatiladi va ishlash tezligiga kuchli ta'sir qiladi.

Boshqa tomondan esa Open Addressingda delete amali, y'ani kalitni o'chirish juda ko'p muammolarni keltirib chiqaradi. Bunda berilgan kalitni shundoqligicha bucketdan o'chirib bo'lmaydi. O'chirishni o'rniga bucketga "o'chirildi" deb belgi qo'yib ketish lozim bo'ladi. Demak, o'chirilgan kalitlar ham bucket egallaydi, bu esa o'z o'rnida boshqa barcha amallar tezligiga ta'sir qiladi.

Chainingda esa bunday muammo yo'q, o'chirilgan elementlar linked-listdan olib tashlanadi. Shuning uchun ham Chaining kattaroq load factorlar bilan ham yaxshi ishlay oladi. Open Addressingda esa, o'chirilgan kalitlar ham load factorga hissa qo'shadi va aslida dictionaryda elementlar kam bo'lsa ham, juda ko'p o'chirish amallari bajarilgani uchun Dictionaryni rehash qilishga to'g'ri kelish mumkin.